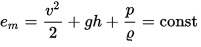बरनोली प्रमेय ( Bernoulli’s theorem )
तरल गतिकी में, बर्नूली का सिद्धान्त (Bernoulli’s principle) या ‘बर्नूली का प्रमेय निम्नवत है:
- किसी प्रवाह में, तरल का वेग बढ़ने पर पर तरल की स्थितिज उर्जा में कमी होती है या उस स्थान पर दाब में कमी हो जाती है। यह सिद्धान्त डच-स्विस गणितज्ञ डैनियल बर्नौली के नाम पर रखा गया है। इस सिद्धान्त की खोज उन्होंने ही की थी और १७३८ में अपनी ‘हाइड्रोडाय्नैमिका’ नामक पुस्तक में प्रकाशित किया था।
बर्नौली समीकरण का विशेष स्थिति में स्वरूप:-
- तरल असंपीड्य (इन्कम्प्रेसिबल) है,
- श्यानता शून्य है,
- स्थाई अवस्था प्राप्त हो गयी है तथा प्रवाह अघूर्णी िर्रोटेशनल) है, तो
जहाँ:
– तरल के ईकाई द्रव्यमान की ऊर्जा
– तरल का घनत्व
– संबन्धित स्थान पर तरल का वेग
– सम्बन्धित स्थान की किसी सन्दर्भ के सापेक्ष ऊँचाई
– गुरुत्वजनित त्वरण
– संबन्धित स्थान पर दाब
अपडेट लगातार हासिल करने के लिए हमे फेसबुक(Facebook) पर ज्वाइन करे Click Now