प्रकाश-परावर्तन एवं अपवर्तन
परावर्तन का नियम
प्रकाश वस्तुओं को दृश्य बनाता है | सूर्य का प्रकाश दिन के समय वस्तुओं के देखने में मदद करता है |
हम किसी वस्तु को कैसे देख पाते है ?
वस्तु पर पड़ने वाले प्रकाश को वस्तु परावर्तित कर देती है, यह परावर्तित किरण जब हमारी आँखों के द्वारा ग्रहण किया जाता है तो यह परावर्तन वस्तु को आँखों के द्वारा देखने योग्य बनाता है |
प्रकाश की किरण : जब प्रकाश अपने प्रकाश के स्रोत से गमन करता है तो यह सीधी एवं एक सरल रेखा होता है | प्रकाश के स्रोत से चलने वाले इस रेखा को प्रकाश की किरण कहते है |
छाया: जब प्रकाश किसी अपारदर्शी वस्तु से होकर गुजरता है तो यह प्रकाश की किरण को परावर्तित कर देता है जिससे उस अपारदर्शी वस्तु की छाया बनती है |
प्रकाश का विवर्तन : यदि प्रकाश के रास्ते में राखी अपारदर्शी वस्तु अत्यंत सूक्ष्म हो तो प्रकाश सरल रेखा में चलने की अपेक्षा इसके किनारों पर मुड़ने की प्रवृति दिखता है – इस प्रभाव को प्रकाश का विवर्तन कहते है |
प्रकाश का परावर्तन :
जब प्रकाश की किरण किसी चमकीले सतह से या परावर्तक पृष्ठ से टकराता है तो यह उसी माध्यम में पुन: मुड़ जाता है जिस माध्यम से यह आता है | इस परिघटना को प्रकाश का परावर्तन कहते है |
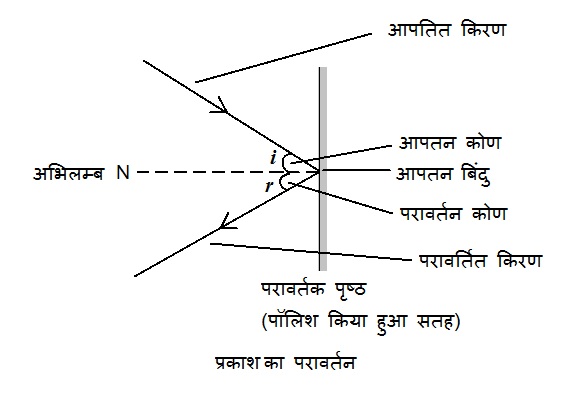
प्रकाश का परावर्तन हमेशा अपारदर्शी वस्तुओं से ही होता है | जबकि प्रकाश का अपवर्तन पारदर्शी वस्तुओं से होता है |
प्रकाश के परावर्तन का नियम :
(i) आपतन कोण, परावर्तन कोण के समान होता है |
∠ i = ∠ r
(ii) आपतित किरण, दर्पण के आपतन बिंदु पर अभिलम्ब और परावर्तित किरण, सभी एक ही तल में होते हैं |
नोट : परावर्तन का यह नियम गोलीय दर्पण सहित सभी परावर्तक पृष्ठों पर लागु होता है |
कुछ समान्य एवं अदभुत परिघटनाएं:
प्रकाश के परावर्तन के कारण कुछ समान्य एवं अदभुत परिघटनाएं होती है जो निम्न है :
दर्पण के द्वारा प्रतिबिम्ब का बनना, तारों का टिमटिमाना, इन्द्रधनुष के सुन्दर रंग, किसी माध्यम द्वारा प्रकाश का मोड़ना आदि |
परावर्तन के प्रकार:
(i) नियमित परावर्तन (specular or regular reflection): इस प्रकार का परावर्तन चिकने सतह से होता है तथा अपतित किरणें परावर्तन के पश्चात् समांतर ही रहती है |
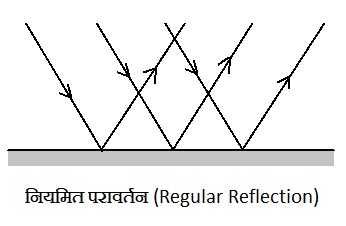
(ii) अनियमित परावर्तन (Diffused or irregular reflection): इस तरह का परावर्तन खुरदरे सतह से होता है तथा परावर्तन के पश्चात् आपतित समान्तर किरणे समान्तर नहीं होती है |

(i) नियमित परावर्तन (specular or regular reflection) :
(ii) विसरित परावर्तन (Diffused or irregular reflection) :
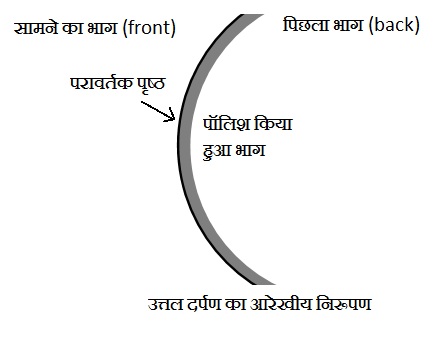
दर्पण : यह एक चमकीला और अधिक पॉलिश किया हुआ परावर्तक पृष्ठ होता है जो अपने सामने रखी वस्तु का प्रतिबिम्ब बनाता है |
दर्पण दो प्रकार का होता है |
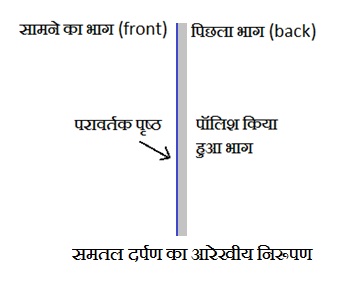
(A) समतल दर्पण (Plane mirror) : इसका परावर्तक पृष्ठ सीधा तथा सपाट होता है |
परिभाषा : ऐसे दर्पण जिनका परावर्तक पृष्ठ समतल हो समतल दर्पण कहलाता है |
(B) गोलीय दर्पण (Spherical mirror) : इसका परावर्तक पृष्ठ वक्र (मुड़ा हुआ) होता है | गोलीय दर्पण का परावर्तक पृष्ठ अन्दर की ओर या बाहर की ओर वक्रित हो सकता है |
परिभाषा : ऐसे दर्पण जिसका परावर्तक पृष्ठ गोलीय होता है, गोलीय दर्पण कहलाता है |
इसी वक्रता के आधार पर गोलीय दर्पण दो प्रकार का होता है |
गोलीय दर्पण के प्रकार :
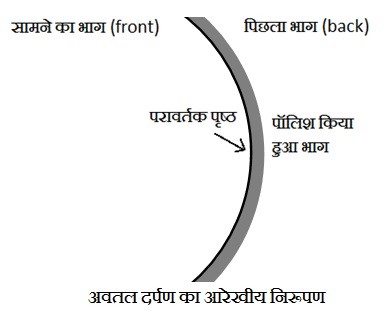
(i) अवतल दर्पण (Concave mirror) : इसका परावर्तक पृष्ठ अन्दर की ओर अर्थात गोले के केंद्र की ओर धसा हुआ (वक्रित) होता है |
(ii) उत्तल दर्पण (convex mirror) : इसका परावर्तक पृष्ठ बाहर की तरफ उभरा हुआ (वक्रित) होता है |
Science Notes के अपडेटेड लगातार हासिल करने के लिए हमें Facebook पर ज्वाईन करे | Click Now
गोलीय दर्पण के भाग:
(i) ध्रुव (Pole): गोलीय दर्पण के परावर्तक पृष्ठ के केंद्र को दर्पण का ध्रुव कहते है | इसे P से इंगित किया जाता है |
(ii) वक्रता केंद्र (Center of Curvature): गोलीय दर्पण का परावर्तक पृष्ठ एक गोले का भाग होता है | इस गोले का केंद्र को गोलीय दर्पण का वक्रता केंद्र कहते है | इसे अंग्रेजी के बड़े अक्षर C से इंगित किया जाता है |
(iii) वक्रता त्रिज्या (The radius of Curvature): गोलीय दर्पण के ध्रुव एवं वक्रता केंद्र के बीच की दुरी को वक्रता त्रिज्या कहते है |
(iv) मुख्य अक्ष (Principal axis): गोलीय दर्पण के ध्रुव एवं वक्रता केंद्र से होकर गुजरने वाली एक सीधी रेखा को दर्पण का मुख्य अक्ष कहते है |
(v) मुख्य फोकस (Principal Focus): दर्पण के ध्रुव एवं वक्रता केंद्र के बीच एक अन्य बिंदु F होता है जिसे मुख्य फोकस कहते है | मुख्य अक्ष के समांतर आपतित किरणें परावर्तन के बाद अवतल दर्पण में इसी मुख्य फोकस पर प्रतिच्छेद करती है तथा उत्तल दर्पण में प्रतिच्छेद करती प्रतीत होती है |
(vi) फोकस दुरी (Focal Length): दर्पण के ध्रुव एवं मुख्य फोकस के बीच की दुरी को फोकस दुरी कहते है, इसे अंग्रेजी के छोटे अक्षर (f ) से इंगित किया जाता है | यह दुरी वक्रता त्रिज्या की आधी होती है |
(vii) द्वारक (Aperture): गोलीय दर्पण का परावर्तक पृष्ठ अधिकांशत: गोलीय ही होता है | इस पृष्ठ की एक वृत्ताकार सीमा रेखा होती है | गोलीय दर्पण के परावर्तक पृष्ठ की इस सीमा रेखा का व्यास, दर्पण का द्वारक कहलाता है |
प्रतिबिम्ब की स्थिति, प्रकृति एवं आकार
बिम्ब की स्थिति : वह स्थान जहाँ वस्तु रखी गई है |
प्रतिबिम्ब की स्थिति : वह स्थान जहाँ दर्पण द्वारा प्रतिबिम्ब बना है |
प्रतिबिम्ब की साइज़ : यह प्रतिबिम्ब का आकार है जो यह बताता है कि वस्तु का प्रतिबिम्ब वस्तु से छोटा बना है, बराबर बना है या वस्तु से बड़ा बना है |
प्रतिबिम्ब की प्रकृति : प्रतिबिम्ब की प्रकृति से यह ज्ञात होता है कि दी गई वस्तु का दर्पण द्वरा बनाया गया प्रतिबिम्ब कैसा है – आभासी या वास्तविक और सीधा या उल्टा |
प्रतिबिम्ब की प्रकृति दो प्रकार का होता है |
(i) वास्तविक और उल्टा : यह प्रतिबिम्ब सदैव दर्पण के सामने एवं उल्टा बनता है |
(ii) आभासी और सीधा : यह प्रतिबिम्ब सदैव दर्पण के परदे के पीछे एवं सीधा बनता है |
अवतल दर्पण द्वारा बनने वाला प्रतिबिम्ब :
अवतल दर्पण में बनने वाली प्रतिबिम्ब वस्तु की स्थिति पर निर्भर करती है | ध्रुव (P) तथा मुख्य फोकस (F) के बीच रखा बिम्ब का ही केवल प्रतिबिम्ब आभासी एवं सीधा बनता है अन्यथा अवतल दर्पण अन्य किसी भी जगह रखी वस्तु का प्रतिबिम्ब वास्तविक एवं उल्टा बनाता है |
- अनंत (infinity) पर रखी वस्तु की प्रतिबिम्ब फोकस F पर वास्तविक एवं उल्टा तथा अत्यधिक छोटा अर्थात बिंदु साइज़ का बनता है |
- वक्रता केंद्र C पर रखी वस्तु की प्रतिबिम्ब फोकस F तथा वक्रता केंद्र C पर वास्तविक एवं उल्टा तथा छोटा बनता है |
- वक्रता केंद्र C पर रखी वस्तु की प्रतिबिम्ब वक्रता केंद्र C पर वास्तविक एवं उल्टा तथा समान साइज़ का बनता है |
- वक्रता केंद्र C एवं मुख्य फोकस F के बीच रखी वस्तु की प्रतिबिम्ब C से परे, वास्तविक एवं उल्टा तथा विवर्धित (बड़ा) बनता है |
- मुख्य फोकस पर रखी वस्तु की प्रतिबिम्ब अनंत (infinity) पर वास्तविक एवं उल्टा एवं अत्यधिक विवर्धित (वस्तु से बहुत बड़ा) बनता है |
- ध्रुव (P) तथा मुख्य फोकस (F) के बीच रखा बिम्ब का प्रतिबिम्ब दर्पण के पीछे आभासी एवं सीधा और वस्तु से बड़ा बनता है
उत्तल दर्पण द्वारा बनने वाला प्रतिबिम्ब :
अवतल दर्पण के उपयोग :
(i) अवतल दर्पणों का उपयोग सामान्यतः टॉर्च, सर्चलाइट तथा वाहनों के अग्रदीपों (headlights) में प्रकाश का शक्तिशाली समांतर किरण पुंज प्राप्त करने के लिए किया जाता है।
(ii) इन्हें प्रायः चेहरे का बड़ा प्रतिबिंब देखने के लिए शेविंग दर्पणों (shaving mirrors) के रूप में उपयोग करते हैं।
(iii) दंत विशेषज्ञ अवतल दर्पणों का उपयोग मरीजों के दाँतों का बड़ा प्रतिबिंब देखने के लिए करते हैं।
(iv) सौर भट्टियों में सूर्य के प्रकाश को केन्द्रित करने के लिए बड़े अवतल दर्पणों का उपयोग किया जाता है।
उत्तल दर्पण का उपयोग :
(i) उत्तल दर्पणों का उपयोग सामान्यतः वाहनों के पश्च.दृश्य (wing) दर्पणों के रूप में
किया जाता है।
(ii) ये दर्पण वाहन के पार्श्व (side) में लगे होते हैं तथा इनमें ड्राइवर अपने पीछे के वाहनों को देख सकते हैं जिससे वे सुरक्षित रूप से वाहन चला सके।
(iii) इसका उपयोग टेलिस्कोप में भी होता है |
(iv) उत्तल दर्पण का उपयोग स्ट्रीट लाइट रिफ्लेक्टर के रूप में भी किया जाता है क्योंकि यह एक बड़े क्षेत्र पर प्रकाश प्रसार करने में सक्षम हैं |
वाहनों में साइड मिरर के रूप उत्तल दर्पण को प्राथमिकता:
उत्तल दर्पणों को इसलिए भी प्राथमिकता देते हैं क्योंकि ये सदैव सीध प्रतिबिंब बनाते हैं यद्यपि वह छोटा होता है। इनका दृष्टि.क्षेत्र भी बहुत अधिक है क्योंकि ये बाहर की ओर वक्रित होते हैं। अतः समतल दर्पण की तुलना में उत्तल दर्पण ड्राइवर को अपने पीछे के बहुत बड़े क्षेत्र को देखने में समर्थ बनाते हैं।
गोलीय दर्पण द्वारा बने प्रतिबिम्ब का निरूपण
- कम से कम दो परावर्तित किरणों के प्रतिच्छेदन से किसी बिंदु बिंब के प्रतिबिंब की स्थिति ज्ञात की जा सकती है।
- प्रतिबिंब के स्थान निर्धरण के लिए निम्न में से किन्हीं भी दो किरणों पर विचार किया जा सकता है।
गोलीय दर्पणों द्वारा परावर्तन के लिए चिन्ह परिपाटी (Sign Convention):
इसे नई चिन्ह परिपाटी भी कहते हैं :
इस चिन्ह परिपाटी के अनुसार :
(i) दर्पण के ध्रुव (P) को मूल बिंदु मानते है, अर्थात दर्पण की सभी दूरियां मूल बिंदु (P) से ही मापी जाती हैं |
(ii) निदेशांक ज्यामिति पद्धति के अनुसार मुख्य अक्ष को x-अक्ष (XX’) लिया जाता है |
(iii) बिंब सदैव दर्पण के बाईं ओर रखा जाता है। इसका अर्थ है कि दर्पण पर बिंब
से प्रकाश बाईं ओर से आपतित होता है।
(iv) मूल बिंदु के दाईं ओर (+ x-अक्ष के अनुदिश) मापी गई सभी दूरियाँ धनात्मक मानी जाती हैं जबकि मूल बिंदु के बाईं ओर (- x-अक्ष के अनुदिश) मापी गई दूरियाँ ऋणात्मक मानी जाती हैं।
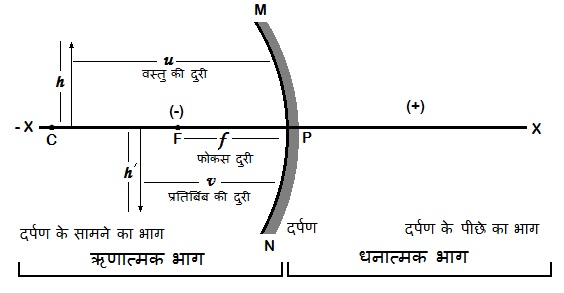
दर्पण के सामने के भाग की सभी दूरियाँ ऋणात्मक (-) ली जाती हैं | और दर्पण के पीछे की सभी दूरियाँ धनात्मक (+) ली जाती हैं |
अवतल दर्पण में : वे सभी दूरियाँ जो दर्पण के सामने होती हैं |
(1) वस्तु की दुरी (u) = – u [ऋणात्मक (-) ली जाती हैं |]
(2) फोकस दुरी (f) = – f [ऋणात्मक (-) ली जाती हैं |]
(3) प्रतिबिंब की दुरी (v) = – v [ऋणात्मक (-) ली जाती हैं, यदि प्रतिबिंब वास्तविक तथा उल्टा बनता हो |]
उत्तल दर्पण में : वे सभी दूरियाँ जो दर्पण के सामने होती हैं एवं जो पीछे होती हैं |
(1) वस्तु की दुरी (u) = – u [ऋणात्मक (-) ली जाती हैं, वैसे वस्तु हमेशा दर्पण के सामने ही रखा जाता है इसलिए u सदैव ऋणात्मक ही होता है |]
(2) फोकस दुरी (f) = f [धनात्मक (+) ली जाती हैं, क्योंकि उत्तल दर्पण की वक्रता पीछे की ओर होता है इसलिए फोकस दुरी भी दर्पण के पीछे होता है |]
(3) प्रतिबिंब की दुरी (v) = v [धनात्मक (+) ली जाती हैं, यदि प्रतिबिंब वास्तविक तथा उल्टा बनता हो तो ऋणात्मक और आभासी एवं सीधा हो तो धनात्मक ली जाती है |]
उत्तल दर्पण ने सदैव आभासी एवं सीधा प्रतिबिम्ब बनता है दर्पण के पीछे बनता है |
दर्पण सूत्र तथा आवर्धन :
बिंब या वस्तु की दुरी : गोलीय दर्पण में दर्पण के सामने रखी वस्तु तथा इसके ध्रुव के बीच की दूरी को बिंब दूरी (u) कहते है। इसे u से दर्शाते हैं |
प्रतिबिम्ब की दुरी: दर्पण के ध्रुव और बने प्रतिबिंब की बीच की दूरी को प्रतिबिंब दूरी (v) कहते हैं | इसे v से दर्शाते हैं |
फोकस दुरी (f) : दर्पण के ध्रुव और मुख्य फोकस के बीच की दुरी को फोकस दुरी कहते हैं |
दर्पण सूत्र : प्रतिबिंब की दुरी (v) का व्युत्क्रम और बिंब की दुरी (u) का व्युत्क्रम का योग फोकस दुरी (f) के व्युत्क्रम के बराबर होता है |

आवर्धन (Magnification): किसी बिंब का प्रतिबिंब कितना गुना बड़ा है या छोटा है यही प्रतिबिंब का आवर्धन कहलाता है |


आवर्धन के लिए बिंब की ऊँचाई धनात्मक ली जाती है, क्योंकि बिंब हमेशा मुख्य अक्ष के ऊपर और सीधा रखा जाता है |
आभासी तथा सीधा प्रतिबिंब के लिए प्रतिबिंब की ऊँचाई (h’) धनात्मक (+) ली जाती है और वास्तविक और उल्टा प्रतिबिंब के लिए बिंब कि ऊँचाई (h’) ऋणात्मक (-) ली जाती है |
आवर्धन का मान : आवर्धन के मान में धनात्मक मान बताता है कि प्रतिबिंब आभासी और सीधा है | ऋणात्मक मान बताता है कि प्रतिबिंब वास्तविक और उल्टा है |
Science Notes के अपडेटेड लगातार हासिल करने के लिए हमें Facebook पर ज्वाईन करे | Click Now
प्रकाश का अपवर्तन
प्रकाश का अपवर्तन : जब प्रकाश की किरण एक माध्यम से दूसरे माध्यम में जाती हैं तो यह अपने मार्ग से विचलीत हो जाती हैं। प्रकाश के किरण को अपने मार्ग से विचलीत हो जाना प्रकाश का अपवर्तन कहलाता हैं ।
प्रकाश का अपवर्तन सिर्फ पारदर्शी पदार्थों से ही होता है | जैसे शीशा, वायु, जल आदि |
प्रकाश के अपवर्तन का कारण : अपवर्तन प्रकाश के एक पारदर्शी माध्यम से दूसरे में प्रवेश करने पर प्रकाश की चाल में परिवर्तन के कारण होता है।
प्रकाश का अपवर्तन का नियम:
प्रकाश का अपवर्तन के नियम दो हैं |
1. आपतित किरण, अपवर्तित किरण तथा आपतन बिन्दु पर अभिलंब तीनों एक ही तल में होते हैं ।
2. जब प्रकाश की किरण किन्हीं दो माध्यमों के सीमा तल पर तिरछी आपतित होती हैं तो आपतन कोण (i) की ज्या (sine) तथा अपवर्तन कोण की ज्या (sine) का अनुपात एक नियतांक होता हैं ।
स्नेल का अपवर्तन का नियम (Snell’s the law of Refraction) : जब प्रकाश की किरण किन्हीं दो माध्यमों के सीमा तल पर तिरछी आपतित होती हैं तो आपतन कोण (i) की ज्या (sine) तथा अपवर्तन कोण की ज्या (sine) का अनुपात एक नियतांक होता हैं । इस नियम को स्नेल का अपवर्तन नियम भी कहते हैं |

अपवर्तन के समय प्रकाश का मार्ग :
जब प्रकाश की किरण एक माध्यम (विरल) से दूसरे माध्यम (सघन) मे जाती हैं तो यह अभिलंब की ओर मुड जाती हैं । जब यही प्रकाश की किरण सघन से विरल की ओर जाती हैं तो अभिलंब से दूर भागती हैं।
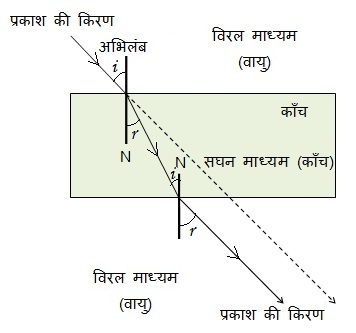
सघन माध्यम (Denser Medium): वह माध्यम जिसका अपवर्तनांक अधिक होता है वह सघन माध्यम कहलाता है | इस माध्यम के कण अधिक घने (dense) होते हैं |
विरल माध्यम (Rarer Medium): वह माध्यम जिसका अपवर्तनांक कम होता है वह विरल माध्यम कहलाता है | इस माध्यम के कणों का घनत्व कम होता है |
- किसी माध्यम का सघन और विरल होना दो माध्यमों में बीच तुलनात्मक अध्ययन है | यह निर्भर करता है कि कौन सा माध्यम किस माध्यम के सापेक्ष अधिक सघन है और कौन सा विरल है |
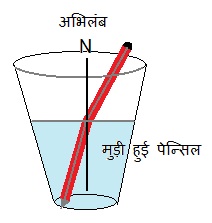
प्रकाश के अपवर्तन से होने वाली परिघतानाएँ:
2. शीशे के गिलास में रखा सिक्का उठा हुआ नजर आना :
ऐसे ही जब हम कोई सिक्का पानी से भरे गिलास में रखते है तो देखते हैं कि सिक्का उठा हुआ नजर आता है ये घटना भी प्रकाश के अपवर्तन के कारण ही होता हैं | अत: यह स्पष्ट हो जाता है कि प्रकाश के अपवर्तन के कारण सिक्का अपनी वास्तविक स्थिति से थोड़ा-सा ऊपर उठा हुआ प्रतीत होता है।
दूसरा उदाहरण है काँच के बर्तन में रखा निम्बू अपने वास्तविक आकार से बड़ा नजर आता है |
- अलग-अलग द्रव्यों (liquids) में पेन्सिल की अथवा प्रकाश का झुकाव अलग-अलग होता है |
- जब प्रकाश एक माध्यम से दूसरे माध्यम में तिरछा होकर जाता है तो दूसरे माध्यम में इसके संचरण की दिशा परिवर्तित हो जाती है।
अपवर्तनांक (Refractive Index) :
जब प्रकाश की किरण एक माध्यम से दूसरे माध्यम में जाती हैं तो यह अपने मार्ग से विचलीत हो जाती हैं। ये विचलन माध्यम और उस माध्यम में प्रकाश की चाल पर निर्भर करता हैं । अतः अपवर्तनांक माध्यमों में प्रकाश की चालों का अनुपात होता है।
“जब प्रकाश की किरण किन्हीं दो माध्यमों के सीमा तल पर तिरछी आपतित होती हैं तो आपतन कोण (i) की ज्या (sine) तथा अपवर्तन कोण की ज्या (sine) का अनुपात एक नियतांक (स्थिरांक) होता हैं । इसी स्थिरांक के मान को पहले माध्यम के सापेक्ष दुसरे माध्यम का अपवर्तनांक (refractive index) कहते हैं |
प्रकाश की चाल और अपवर्तनांक : किसी भी माध्यम में प्रकाश की चाल उसके अपवर्तनांक पर निर्भर करता है | माध्यम का
Science Notes के अपडेटेड लगातार हासिल करने के लिए हमें Facebook पर ज्वाईन करे | Click Now
गोलीय लेंसों द्वारा अपवर्तन
लेंस (Lens) : दो पृष्ठों से घिरा हुआ कोई पारदर्शी माध्यम जिसका एक या दोनों पृष्ठ गोलीय है, लेंस कहलाता है |
उत्तल लेंस (Convex Lens) : वह लेंस जिसके दोनों बाहरी गोलीय पृष्ठों का उभार बाहर की ओर हो उसे उत्तल लेंस कहते हैं | इस लेंस को अभिसारी लेंस भी कहते हैं क्योंकि यह अपने से गुजरने वाले प्रकाश किरणों को अभिसरित कर देता है |
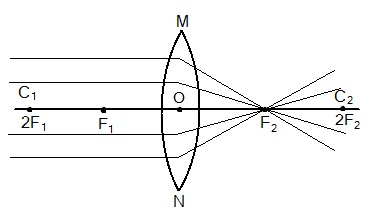
उत्तल लेंस (Convex Lens)
अवतल लेंस (Concave Lens) : वह लेंस जिसके दोनों बाहरी गोलीय पृष्ठ अंदर की ओर वक्रित हो उसे अवतल लेंस कहते हैं | इस लेंस को अपसारी लेंस भी कहते हैं क्योंकि यह अपने से गुजरने वाले प्रकाश किरणों को अपसरित कर देता है |
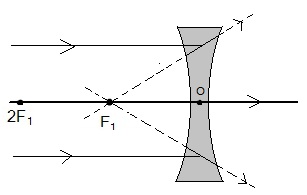
अवतल लेंस (Concave Lens)
वक्रता केंद्र (Centre of curvature) : सभी गोलीय लेंस के प्रत्येक पृष्ठ एक गोले के भाग होते हैं | इन गोलों के केंद्र को लेंस का वक्रता केंद्र कहते है | इसे C1 तथा C2 से दर्शाते हैं |
मुख्य अक्ष (Principle Axis) : मुख्य अक्ष किसी लेंस के दोनों वक्रता केन्द्रों से गुजरने वाली एक काल्पनिक सीधी रेखा लेंस की मुख्य अक्ष कहलाती है।
प्रकाशिक केंद्र (Optic Centre) : लेंस का केन्द्रीय बिंदु इसका प्रकाशिक केंद्र कहलाता है। इसे प्रायः अक्षर O से निरूपित करते हैं।
लेंस के प्रकाशिक केंद्र से गुजरने वाली प्रकाश किरण बिना किसी विचलन के निर्गत होती है।
द्वारक (Aperture) : गोलीय लेंस की वृत्ताकार रूपरेखा का प्रभावी व्यास इसका द्वारक (aperture) कहलाता है।
पतले लेंस : ऐसे लेंस जिनका द्वारक इनकी वक्रता त्रिज्या से बहुत छोटा है। ऐसे लेंस छोटे द्वारक के पतले लेंस कहलाते हैं।
उत्तल लेंस का मुख्य फोकस (Principle Focus) : उत्तल के पर मुख्य अक्ष के समांतर प्रकाश की बहुत सी किरणें आपतित हैं। ये किरणें लेंस से अपवर्तन के पश्चात मुख्य अक्ष पर एक बिंदु पर अभिसरित हो जाती हैं। मुख्य अक्ष पर यह बिंदु लेंस का मुख्य फोकस (Principle Focus) कहलाता है।
अवतल लेंस का मुख्य फोकस (Principle Focus) : अवतल लेंस पर मुख्य अक्ष के समांतर प्रकाश की अनेक किरणें आपतित होती हैं। ये किरणें लेंस से अपवर्तन के पश्चात मुख्य अक्ष के एक बिंदु से अपसरित होती प्रतीत होती हैं। मुख्य अक्ष पर यह बिंदु अवतल लेंस का मुख्य फोकस कहलाता है।
लेंस का फोकस दुरी (Focal Distance) : किसी लेंस के मुख्य फोकस की प्रकाशिक केन्द्र से दूरी फोकस दूरी कहलाती है।
गोलीय लेंसों के लिए चिन्ह-परिपाटी :
(i) गोलीय लेंसों में सभी दूरियाँ प्रकाशिक केन्द्रों (optic centre) से मापी जाती है |
(ii) उत्तल लेंस की फोकस दुरी धनात्मक (+) होती हैं |
(iii) अवतल लेंस की फोकस दुरी ऋणात्मक (-) होती हैं |
(iv) जिस ओर से प्रकाश लेंस में प्रवेश करता है उस भाग को ऋणात्मक माना जाता है | चाहे वो उत्तल लेंस हो या अवतल लेंस हो | अर्थात जिधर हम बिंब (object) को रखते है वो भाग ऋणात्मक होता है |
(v) लेंस में सभी वास्तविक एवं उल्टा प्रतिबिंब को धनात्मक लेते हैं | और आभासी एवं सीधा प्रतिबिंब को ऋणात्मक लेते है |
(vi) वास्तविक एवं उल्टा प्रतिबिंब लेंस के धनात्मक भाग में बनते हैं और आभासी एवं सीधा प्रतिबिंब लेंस के ऋणात्मक भाग में बनते है |
(vii) बिंब की ऊंचाई (h) सीधा होता है इसलिए इसे धनात्मक (+) लेते हैं | प्रतिबिंब सीधा है तो आभासी और सीधा यदि प्रतिबिंब (h’) उल्टा हो तो वास्तविक और उल्टा इसे ऋणात्मक (-) लेते है |
लेंस में आवर्धन (Magnification in Lens) :
लेंस की क्षमता
लेंस की क्षमता : किसी लेंस द्वारा प्रकाश किरणों को अभिसरण और अपसरण करने की मात्रा (degree) को लेंस की क्षमता कहते हैं | यह उस लेंस के फोकस दुरी के व्युत्क्रम के बराबर होता है | इसे P द्वारा व्यक्त किया जाता है और इसका S.I मात्रक डाइऑप्टर (D) होता है |

1 डाइऑप्टर (D) = 1 m या 100 cm के बराबर होता है |
यदि फोकस दुरी (f) को मीटर में व्यक्त करें तो क्षमता जो ‘डाइऑप्टर’ (Dioptre) में व्यक्त किया जाता है |
उत्तल लेंस की क्षमता धनात्मक (+) होती है |
अवतल लेंस की क्षमता ऋणात्मक (-) होती है |
उदाहरण : मान लीजिये कि एक लेंस की क्षमता + 2 D है | इसका अर्थ यह है कि वह उत्तल लेंस है और उसकी फोकस दुरी (f) + 0.50 m है अर्थात + 50 सेमी है |
और यदि एक अन्य लेंस की क्षमता -2 D है तो वह अवतल लेंस है और उसकी फोकस दुरी (f) – 0.50 m है अर्थात – 50 सेमी है |
लेंस की क्षमता से प्रश्न:
उदाहरण 1. एक अवतल लेंस जिसकी फोकस दुरी 25 cm है इसकी क्षमता ज्ञात कीजिये |
हल : फोकस दुरी (f) = – 25 cm = – 0.25 m (अवतल लेंस की क्षमता ऋणात्मक होती है |)

= 1/0.25
= 4 D
उदाहरण 2. एक उत्तल लेंस जिसकी फोकस दुरी 40 सेमी है इस लेंस की क्षमता ज्ञात कीजिये |
हल : फोकस दुरी (f) = 40 cm = 0.4 m

= 1/0.4
= 10/4
= 2.5 D
लेंस की क्षमता
लेंस की क्षमता : किसी लेंस द्वारा प्रकाश किरणों को अभिसरण और अपसरण करने की मात्रा (degree) को लेंस की क्षमता कहते हैं | यह उस लेंस के फोकस दुरी के व्युत्क्रम के बराबर होता है | इसे P द्वारा व्यक्त किया जाता है और इसका S.I मात्रक डाइऑप्टर (D) होता है |

1 डाइऑप्टर (D) = 1 m या 100 cm के बराबर होता है |
यदि फोकस दुरी (f) को मीटर में व्यक्त करें तो क्षमता जो ‘डाइऑप्टर’ (Dioptre) में व्यक्त किया जाता है |
उत्तल लेंस की क्षमता धनात्मक (+) होती है |
अवतल लेंस की क्षमता ऋणात्मक (-) होती है |
उदाहरण : मान लीजिये कि एक लेंस की क्षमता + 2 D है | इसका अर्थ यह है कि वह उत्तल लेंस है और उसकी फोकस दुरी (f) + 0.50 m है अर्थात + 50 सेमी है |
और यदि एक अन्य लेंस की क्षमता -2 D है तो वह अवतल लेंस है और उसकी फोकस दुरी (f) – 0.50 m है अर्थात – 50 सेमी है |
लेंस की क्षमता से प्रश्न:
उदाहरण 1. एक अवतल लेंस जिसकी फोकस दुरी 25 cm है इसकी क्षमता ज्ञात कीजिये |
हल : फोकस दुरी (f) = – 25 cm = – 0.25 m (अवतल लेंस की क्षमता ऋणात्मक होती है |)

= 1/0.25
= 4 D
उदाहरण 2. एक उत्तल लेंस जिसकी फोकस दुरी 40 सेमी है इस लेंस की क्षमता ज्ञात कीजिये |
हल : फोकस दुरी (f) = 40 cm = 0.4 m

= 1/0.4
= 10/4
= 2.5 D
Science Notes के अपडेटेड लगातार हासिल करने के लिए हमें Facebook पर ज्वाईन करे | Click Now
// ]]>

